Dr Konstantin Leyde (University of Portsmouth)

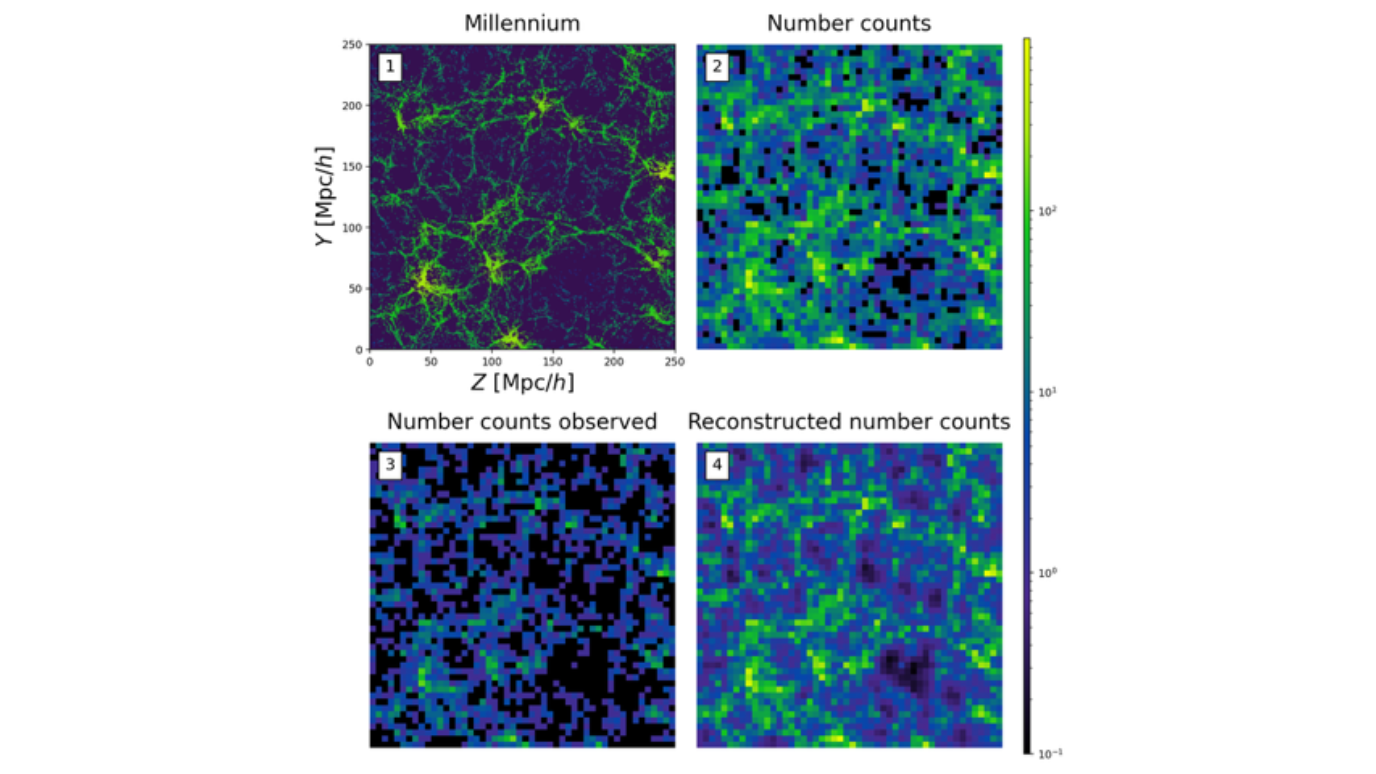
Compact binary coalescences that are observed through gravitational waves (GWs) provide an independent probe to constrain the current expansion rate of the Universe, H0. In addition to the information on the luminosity distance directly provided by the GW, redshift information is also needed for the H0 measurement. Except for the binary neutron star merger GW170817, no GW event was accompanied by a direct electromagnetic counterpart, and other methods are needed to provide the redshift information. I will summarize two methods that offer a solution to this problem. Since these approaches require no additional electromagnetic redshift, they allow one to constrain H0 from all detected GW sources. (i) The first one uses the (redshifted) source frame mass distribution, also known as the mass spectrum method. Since the source frame mass distribution is unknown, one has to marginalize over the associated parameters. (ii) The so-called dark sirens method leverages the overlap of the GW sky position and galaxy catalogs into redshift information. However, currently used galaxy catalogs include only the bright end of the galaxy distribution and, therefore, provide little redshift information. I will show that from such a magnitude-limited galaxy catalog, one can probabilistically reconstruct the full galaxy field, using knowledge of the spatial correlation of galaxies quantified by the dark matter power spectrum. This completed galaxy catalog (including the estimated faint galaxy counts in each voxel) should result in a tighter H0 measurement. In the second half of my talk, I will summarize how one can apply neural posterior estimation for fast-and-accurate hierarchical Bayesian inference of the mass spectrum method. We use a normalizing flow to estimate directly the posterior of the source frame mass parameters from a a catalog of GW events. This approach provides complete freedom in event representation, automatic inclusion of selection effects, and (in contrast to likelihood estimation) without the need for stochastic samplers to obtain posterior samples. Since the number of events may be unknown when the network is trained, we split our analysis into sub-population analyses that we later recombine; this allows for fast sequential analyses as additional events are observed.